En ELU (état limite ultime), il est nécessaire de vérifier les contraintes dans la structure (cf Eurocode 0 > ELU).
En calcul acier, on distingue les contraintes de traction/compression, de flexion et de cisaillement (efforts tranchants + torsion). En calcul bois, en raison du caractère orthotrope du bois, on distingue davantage de types de contraintes, les résistances du bois étant variables : traction axiale, traction tranversale, compression axiale avec flambement, compression transversale, compression oblique, flexion simple, cisaillement, puis sollicitations composées (flexion+traction, flexion+compression, flexion déviée, flexion déviée+compression).
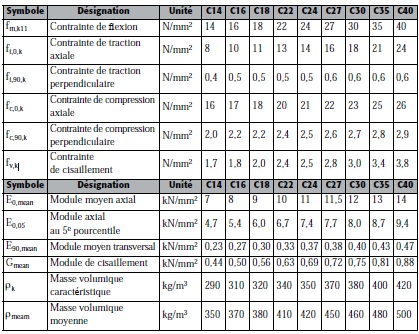
Données pour déterminer les contraintes admissibles
 |
|

Valeur du coefficient kmod pour bois massif, lamellé-collé, lamibois et contreplaqué (valeur sélectionnée en fonction de la charge la plus courte)
Le coefficient γM est quant à lui fonction de la dispersion du matériau : γM = 1.3 pour le bois / 1.25 pour le lamellé collé / 1.2 pour le lamibois
Contrainte admissible pour les différents types de sollicitation dans une poutre de sections hxb (h = plus grande dimension)
Traction axiale |
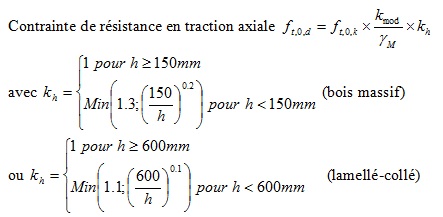 |
Exemple : charpente abritée, non chauffée, altitude < 1000m, bois C24 section 122x36, avec 10 000N de traction
σ = 10 000 / 122 / 36 = 2.28 MPa
ft,0,d = 14 x 0.9 / 1.3 x (150/122)^0.2 = 10.10 MPa
D'où un taux de travail 2.28/10.10 = 23 %
|
Traction transversale |
Sollicitation présente essentiellement dans les assemblages inclinés, les angles de portiques en bois LC et dans la partie basse des poutres courbes |
- |
Compression axiale avec flambement |
m = coefficient de flambement = 2 pour encastré/libre, 1 pour rotulé/rotulé, 0.7 pour encastré/rotulé et 0.5 pour encastré/encastré Le risque de flambement est considéré si λrel > 0.3. |
Exemple : poteau de 3.2m, considéré rotulé aux extrémités, exposé aux intempéries, C18 avec section 150x100, compression de 20 000 N
A = 150x100 = 15 000mm² I = 100^3x150/12 = 12 500 000mm4 λrel = 1 x 3200 / Pi x racine(15000x18/12500000/6000) = 1.933 > 0.3 --> risque de flambage k = 0.5 x (1+0.2x(1.933-0.3)+1.933²) = 2.53 kc = 1 / (2.53 + racine(2.53²-1.933²)) = 0.24 fc,0,d = 18 x 0.7 / 1.3 = 9.69 MPa Taux de travail : 20000 / A / (0.24x9.69) = 57 % |
Compression transversale |
Action perpendiculaire aux fibres --> appuis d'une poutre + certains assemblages La contrainte dépend de la surface de l'appui (d = longueur de l'appui de la pièce)
Le coefficient kc,90 permet de majorer la résistance (il est compris entre 1 et 4) |
Exemple : solive section 200x75 bois C24, portée 4.5m, entraxe 0.5m, local chauffé, charge maximale de 292.5 daN/m², longueur appui 50mm
σ = 2925x0.5x4.5/2/50/75 = 0.88 MPa fc,90,d = 5.3 x 0.8 / 1.3 = 3.26 MPa on suppose que kc,90 = 2.9 d'où taux de travail = 0.88 / (2.9x3.26) = 9% |
Compression oblique |
Pièce de bois recevant une action inclinée par rapport aux fibres (assemblages tels embrèvements), contrefiches, etc... La contrainte de résistance en compression oblique est comprise entre la contrainte de compression axiale et la contrainte de compression transversale (formule de Hankinson) :
α est l'angle entre l'effort et le fil du bois |
Exemple : poteau section 200x200, arêtier 150x450 en bois LC (GL28h), local chauffé, charge totale 43 500N, pente arêtier 19.3°, longueur de l'appui de l'arêtier sur le poteau = 136mm
σ = 43500 / 136/150 = 2.13 MPa fc,90,d = 3 x 0.9/1.25 = 2.16 MPa et kc,90 = 1 fc,0,d = 26.5 x 0.9 / 1.25 = 19 MPa
Taux travail = 2.13 x (19/2.16 x sin²70.7+cos²70.7) / 19 = 89% |
Flexion simple avec déversement |
lef = longueur efficace = L x klef Appuis simples : klef = 0.9 en charge répartie et 0.8 en charge concentrée Porte à faux : klef = 0.5 en charge répartie et 0.8 en charge concentrée Si poutre chargée sur fibre comprimée : lef est augmentée de 2h Si poutre chargée sur fibre tendue : lef est diminuée de 0.5h ksys = coef d'effet système = 1 ou 1.1 (effet système lorsque plusieurs éléments porteurs de mêmes nature et fonction sont sollicités par un même type de chargement répartie uniformément) |
Exemple : solive en bois massif section 50x200 bois C24, de longueur 5m, comble non chauffé, moment maximal 3 825 N.m (charge en partie répartie)
σm,crit = 0.78 x 7400 x 50² / 200 / (0.9x5000+2x200) = 14.72 MPa λrel,m = racine(24/14.72) = 1.277 > 0.75 et < 1.4 kcrit = 1.56 - 0.75 x 1.277 = 0.602 fmd = 24 x 0.9/1.3 x 1 x 1 = 16.62 MPa
Taux de travail : 3825000 / (200²x50/6) / (0.602 x 16.62) = 115%
|
Cisaillement |
Sollicitation rencontrée au droit des appuis dans les poutres en flexion :
kv = coefficient d’entaillage = 1 si entaille dans zone comprimée (généralement partie supérieure de la poutre) ou si la pente de l’entaille est inférieure à 10% |
Exemple : solive bois massif section 75x225 bois C24, portée 5m, entraxe solive 0.5m, local chauffé, avec charge totale 292.5 daN/m² (sans entaille)
fv,d = 2.5 x 0.8 / 1.3 = 1.54 MPa
σcisaillement = (0.5x2925x5/2) / (225x75x2/3) = 0.325 MPa
Taux de travail = 0.325 / 1.54 = 21% |
Sollicitations combinées
Flexion + traction |
Le déversement n'est pas considéré dans ce cumul (kcrit = 1).
|
Exemple : pièce section 200x50 bois C24, pente 26.6°, portée 5m, entraxe 0.5m, zone non chauffée, charge totale 195.8 daN/m²
Traction : σ = 1958x0.5xsin26.6°x5/200/50 = 0.22 MPa ft0d = 14x0.9/1.3x1 = 9.69 Mpa Taux = 2.3%
Flexion : σ = 1958x0.5xcos26.6°x5²x1000/8/(200²x50/6) = 8.21 MPa fmd = 24 x 0.9 / 1.3 x 1.1 x 1 = 18.28 MPa Taux = 45%
Taux combiné = 47.3 % |
Flexion + compression |
Le déversement et le flambement sont pris en compte (kcrit et kc).
|
Même exemple que précédemment avec compression dans la pièce au lieu de traction (on limite la longueur de flambement et de déversement à 1667mm, avec des entretoises)
Compression avec flambement A = 200x50 = 10 000 mm² et I = 200x50^3/12 = 2 083 333 mm4 λ = 1 x 1667 / Pi x racine(10000x21/2083333/7400) = 1.958 > 0.3 k = 0.5 x (1+0.2x(1.958-0.3)+1.958²) = 2.61 kc = 1 / (2.61 + racine(2.61²-1.958²)) = 0.231 fc,0,d = 21 x 0.9 / 1.3 = 14.54 MPa Taux de travail : 2192 / A / (0.231x14.54) = 6.5 %
Flexion avec déversement σm,crit = 0.78 x 7400 x 50² / 200 / (1667+2x200) = 34.91 MPa λrel,m = racine(24/34.91) = 0.829 > 0.75 et < 1.4 kcrit = 1.56 - 0.75 x 0.829 = 0.938 Taux de travail : 8.21 / (0.938 x 18.28) = 48 %
Taux combiné : 0.0605 + 0.048² = 29% |
Flexion déviée |
Elle se rencontre par exemple dans les pannes posées à dévers.
km = 0.7 pour les sections rectangulaires |
Exemple : pannes à dévers section 100x200 bois C24, pente 17°, portée 3.5m, entraxe 1.8m, zone non chauffée, charge 209.3 daN/m²
σfy = (2093x1.8xcos17°x3.5²x1000/8) / (200²x100/6) = 8.28 MPa σfz = (2093x1.8xsin17°x3.5²x1000/8) / (100²x200/6) = 5.06 MPa fmd = 24 x 0.9/1.3 = 16.6 Mpa Taux de travail = 0.7 x 5.06/16.6 + 8.28/16.6 = 71% |
Flexion déviée et comprimée |
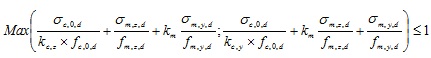 |
Même exemple que précédemment avec en plus du vent provoquant une poussée (compression supposée de 15 000 N)
Compression avec flambement z A = 200x100 = 20 000 mm² et Iz = 200x100^3/12 = 16 666 666 mm4 λz = 1 x 3500 / Pi x racine(20000x21/16666666/7400) = 2.056 > 0.3 kz = 0.5 x (1+0.2x(2.056-0.3)+2.056²) = 2.79 kcz = 1 / (2.79 + racine(2.79²-2.056²)) = 0.214 Compression avec flambement y A = 200x100 = 20 000 mm² et Iy = 200^3x100/12 = 66 666 666 mm4 λy = 1 x 3500 / Pi x racine(20000x21/66666666/7400) = 1.028 > 0.3 ky = 0.5 x (1+0.2x(1.028-0.3)+1.028²) = 1.10 kcy = 1 / (1.10 + racine(1.10²-1.028²)) = 0.67
fc,0,d = 21 x 1.1 / 1.3 = 17.78 MPa (kmod = 1.1 car la durée de la charge la plus courte est instantanée, le vent en l'occurence) fmd = 24 x 1.1/1.3 = 20.3 Mpa
Taux de travail : 15000 / 20000 / (0.214x17.78) + 0.7x8.28/20.3 + 5.06/20.3 = 73% |