Depuis la version 9.0.0, l'Eurocode 5 ("Conception et calcul des structures en bois" - NF EN 1995-1-1 de novembre 2005) est implémenté dans Freelem.
Le logiciel calcule les déplacements en intégrant le fluage (ELS), et les différents ratios de contraintes ELU (cisaillement, compression avec flambement, flexion avec déversement, traction, et les ratios combinés). Certaines vérifications ne sont pas faites (traction transversale, compression transversale, compression oblique).
Comment cela fonctionne ?
1ère étape : allez dans Codes et choisissez Eurocode 5. Choisissez l'humidité (assez impactant sur les résultats), c'est à dire la classe de service.
2ème étape : la modélisation en elle-même.
Les différences par rapport à une modélisation sans code implémenté se situent dans l'onglet des barres, et l'onglet des chargements.
Dans l'onglet des barres, vous devez définir de nouveaux paramètres : les 2 coefficients de flambement, les 2 longueurs de flambement (hors plan et dans le plan), les 2 longueurs de déversement, et la case Auto (si vous la cochez, toutes les longueurs sont prises égales à la longueur de la barre).
Dans l'onglet des chargements, vous choisissez la nature de la charge : Permanentes, Exploitation, Vent, Neige normale <1000m, Neige normale >1000m, et Neige exceptionnelle. A la charge est associée une durée d'application (permanente, long terme, moyen terme, court terme, et instantanée), et un coefficient dit kmod qui joue directement sur les résistances du bois.
3ème étape : il n'y a plus qu'à lancer le calcul, qui vous donnera le ratio maximal dans la structure. En générant la note, les détails des calculs apparaitront, avec l'affichage des calculs intermédiaires.
Pour le calcul des différents ratios, il faut que toutes les données matériaux soient définies dans le catalogue (cliquer ).
Par ailleurs, le logiciel ne peut calculer les ratios que si : les poutres bois sont rectangulaires ou moisées, et le matériau est de type bois. Si l'une de ces conditions n'est pas respectée, aucun ratio n'est calculé.
Remarque : pour le fluage (en état limite de service) :
ψ2=1 pour les charges permanentes
ψ2 = 0.8 pour les charges d'exploitation (valeur maximale)
ψ2 = 0 pour le vent, la neige exceptionnelle et la neige normale <1000m
ψ2 = 0.2 pour la neige normale >1000m
kdef = 0.6 pour la classe de service 1 (humidité <13%)
kdef = 0.8 pour la classe de service 2 (humidité entre 13% et 20%)
kdef = 2 pour la classe de service 3 (humidité >20%)
Pour la résistance en état limite ultime :
ksys = 1
γM = 1.3 pour le bois massif et 1.25 pour le lamellé collé
Pour les pièces moisées, les élancements (flambement) sont divisés par 2, et la contrainte critique de déversement également.
Pour le calcul de kmod, la valeur dépend de la durée du chargement et de la classe de service. Les kmod sont identiques pour les classes de service 1 et 2. Pour les combinaisons, le kmod est calculé à partir de la charge la plus courte (le kmod est donc la valeur maximale des kmod associés aux chargements élémentaires de la combinaison traitée).
Exemples de calculs
Les résultats ont été testés sur 13 cas de calculs : 2 cisaillement, 1 flambement, 2 traction, 4 flexion, 1 flexion+traction, 1 flexion+compression, 1 flexion déviée, et 1 flexion déviée comprimée.
Attention aux longueurs d'instabilité (flambement et déversement), que seul le concepteur de l'ouvrage peut connaître et maîtriser. Ne confondez pas longueur de la barre maillée et longueur réelle d'instabilité ! Par exemple, si vous étudiez le flambement d'une poutre encastrée chargée en son extrémité par une force de compression, rien ne vous empêche de découper la poutre en x éléments. Si vous cochez sur Auto sur chacun de ces x éléments, vous étudierez le flambement sur la longueur des éléments maillés, et non la longueur réelle, qui est la longueur totale/physique de la barre. Par ailleurs, pensez à tenir compte des éléments stabilisés pour stabiliser les éléments étudiés. Exemple : arbalétrier stabilisé par les pannes si ces dernières sont stabilisées. L'arbalétrier déverse alors non pas sur la longueur totale, mais sur une longueur égale à l'entraxe entre pannes, ces dernières constituant des maintiens latéraux. Idem pour le flambement hors plan.
Enfin, vous pouvez définir la longueur efficace de déversement avec la formule suivante : Ldev = 0.9L + 2h (L étant la longueur physique de déversement, 0.9 un coefficient associé à une charge répartie, et la majoration 2h avec h = hauteur section est une majoration liée au fait que la charge est supposée appliquée sur la fibre comprimée). Exemple : barre 200x80 pouvant déverser sur 2 mètres --> Ldev = 0.9x2 + 2x0.2 = 2.2m
Remarque : pour le déversement, le logiciel prend en compte le Max des longueurs de déversement définies (sup et inf) pour le calcul.
| Traction1 | 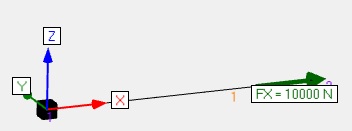 |
Humidité entre 13% et 20% REC122x36 Bois résineux C24 Traction de 10 000 N dû à la neige <1000m
|
Ratio ELU 0.23 |
| Traction2 | 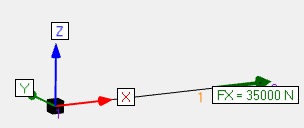 |
Humidité entre 13% et 20% REC200x100 Bois lamellé collé GL28h Traction de 35 000 N dû au vent |
Ratio ELU 0.09 |
| Compression | 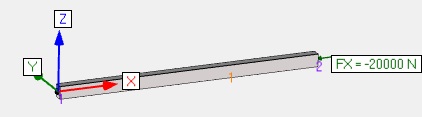 |
Humidité > 20% REC150x100 de 3.2m de long Bois résineux C18 Compression de 20 000 N dû à la neige <1000m |
Ratio ELU 0.57 |
| Flexion1 | 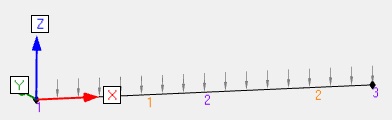 |
Humidité < 13% Poutre de 4.5m de long sur 2 appuis REC200x75 Bois résineux C24 Pas de déversement considéré Effort linéique permanent G = -0.25 N/mm Effort linéique d'exploitation Q = -0.75 N/mm ELS : G+Q et ELU : 1.35G+1.5Q |
Flèche totale DZ en ELS avec fluage : DZ = 14.66mm ( ψ2 = 0.8)
Ratio ELU 0.50
|
| Flexion2 - 1 | 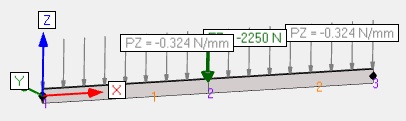 |
Humidité entre 13% et 20% Poutre de 5m de long sur 2 appuis REC200x50 Bois résineux C24 Déversement sur longueur 2650mm (entretoise à mi-portée donc L = 0.9x2500+2x200 = 2650mm) Effort linéique permanent G = -0.24 N/mm Effort nodal neige<1000m S = -1500 N ELS : G+S et ELU : 1.35G+1.5S |
Flèche totale DZ en ELS avec fluage : DZ = 20.24mm
Ratio ELU = 0.81 |
| Flexion2 -2 |  |
Humidité entre 13% et 20% Poutre de 5m de long sur 2 appuis REC200x50 Bois résineux C24 Déversement sur longueur 4900mm (0.9x5000+2x200 = 4900mm) Effort linéique permanent G = -0.24 N/mm Effort nodal neige<1000m S = -1500 N ELS : G+S et ELU : 1.35G+1.5S |
Ratio ELU = 1.15 |
| Flexion3 | 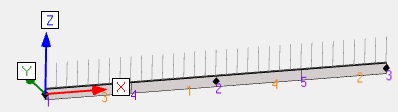 |
Humidité entre 13% et 20% Poutre de 6.6m de long sur 3 appuis REC200x50 Bois résineux C24 Déversement sur longueur 3370mm (0.9x3300+2x200 = 3370mm) Effort linéique permanent G = -0.75 N/mm Effort linéique neige<1000m S = -1.05 N/mm ELS : G+S et ELU : 1.35G+1.5S |
Flèche totale DZ en ELS avec fluage : DZ = 4.04mm
Ratio ELU = 0.83 |
| Cisaillement1 | 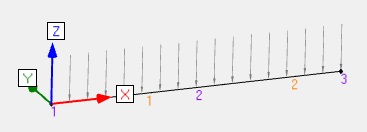 |
Humidité < 13% Poutre de 5m de long sur 2 appuis REC225x75 Bois résineux C24 Effort linéique permanent G = -0.25 N/mm Effort linéique exploitation Q = -0.75 N/mm ELS : G+Q et ELU : 1.35G+1.5Q |
Ratio ELU = 0.21 (cisaillement, ce n'est pas le ratio maximal) |
| Cisaillement2 | 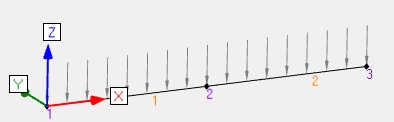 |
Humidité entre 13% et 20% Poutre de 6.6m de long sur 3 appuis REC200x63 Bois résineux C24 Effort linéique permanent G = -0.75 N/mm Effort linéique neige<1000m S = -1.05 N/mm ELS : G+S et ELU : 1.35G+1.5S |
Ratio ELU = 0.37 (cisaillement, ce n'est pas le ratio maximal) |
| Flexion+traction | 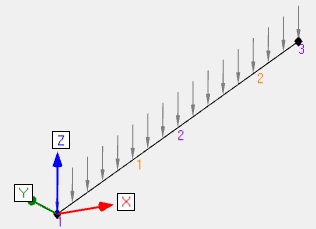 |
Humidité entre 13% et 20% Poutre de 5m de long sur 2 appuis, inclinée d'un angle de 26.6° REC200x50 Bois résineux C24 Effort linéique permanent G = -0.225 N/mm Effort linéique neige<1000m S = -0.45 N/mm ELS : G+S et ELU : 1.35G+1.5S
|
Flèches totales en ELS avec fluage : DX = 7.58mm DZ = 15.17mm Soit D = 16.96mm en somme quadratique
Ratio ELU = 0.49 |
Flexion+ compression |
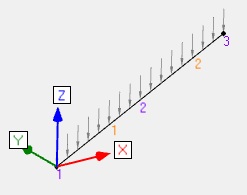 |
Humidité entre 13% et 20% Poutre de 5m de long sur 2 appuis, inclinée d'un angle de 26.6° REC200x50 Bois résineux C24 Flambement dans le plan sur 5000mm Flambement hors plan limité à 1667mm Déversement sur 2067mm (1667+2x200=2067mm) Effort linéique permanent G = -0.225 N/mm Effort linéique neige<1000m S = -0.45 N/mm ELS : G+S et ELU : 1.35G+1.5S |
Ratio ELU = 0.28 (flexion+compression) |
| Flexion déviée | 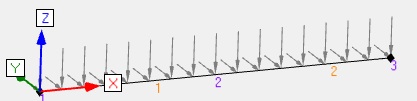 |
Humidité entre 13% et 20% Poutre de 3.5m de long sur 2 appuis REC200x100 Bois résineux C24 Effort linéique permanent G = -0.95 N/mm en inertie forte et -0.29N/mm en inertie faible Effort linéique neige<1000m S = -1.55 N/mm en inertie forte et -0.474N/mm en inertie faible ELS : G+S et ELU : 1.35G+1.5S |
Flèches totales en ELS avec fluage : DY = -10.62mm DZ = -8.69mm Soit D = 13.7mm en somme quadratique
Ratio ELU = 0.71 |
Flexion déviée comprimée |
 |
Humidité entre 13% et 20% Poutre de 3.5m de long sur 2 appuis REC200x100 Bois résineux C24 Flambement sur 3500mm Effort linéique permanent G = -0.95 N/mm en inertie forte et -0.29N/mm en inertie faible Effort linéique neige<1000m S = -1.55 N/mm en inertie forte et -0.474N/mm en inertie faible Compression de W = 30 000 N due au vent ELS : G+S et ELU : 1.35G+1.5S+0.9W |
Ratio ELU = 0.71 |