Les effets de la neige suivant la nouvelle réglementation Eurocode 1 sont expliqués dans la page dédiée Eurocode>Eurocode 1>Neige.

 

 

Les effets de la neige dépendent de plusieurs facteurs :

 

 

1. de la région où se situe la construction

 

Région s0min (daN/m²) s0a (daN/m²)
1A 45 -
1B 45 100
2A 55 100
2B 55 135
3 65 135
4 90 180

 

 

 

 

s0a correspond à la charge accidentelle.

Cette dernière ne s'applique qu'au cas I (cf point 3 de cette page).

 

 

 

2. de l'altitude :

 

h
s0 en daN/m²
h ≤200m s0min
200m<h ≤ 500m s0min + (0.15h-30)

500m<h ≤1000m

 s0min + (0.3h-105)
1000m<h ≤2000m s0min + (0.45h-255)
Nota : l'effet de l'altitude ne s'applique pas à la charge accidentelle.

 

 

 

3. de la forme de la toiture et du vent : ces paramètres vont jouer sur l'accumulation de la neige, et sont caractérisés par le coefficient de forme μ.

Ci-dessous un tableau récapitulatif de calcul de ce coefficient pour une toiture à 2 versants :

 

Cas
Mode de répartition

Toiture simple à 2 versants plans

(sans dispositifs de retenue)

Valeurs de μ en fonction de l'angle β de la toiture
I
 Charge de neige répartie sans redistribution par le vent (vent faible)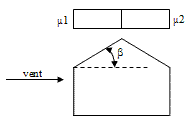

0 ≤ β ≤ 30° --> μ1 = μ2 =0.8

 

30° < β < 60° --> μ1 = μ2 = 0.8 - 0.8( β-30)/30

 

β ≥ 60° --> μ1 = μ2 = 0
II
 Charge de neige répartie après redistribution par le vent (vent modéré à partir de 6 m/s)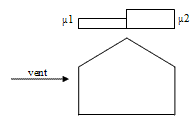

0 ≤ β ≤ 15° --> μ1 = μ2 = 0.8

 

15° < β ≤30° --> μ1 = 0.8 - 0.4( β-15)/15

μ2 = 0.8 + 0.4( β-15)/15 ( μ2 = 1 pour 22.5° < β<35°)

 

30°< β ≤ 60° --> μ1 = 0.4 - 0.4( β-30)/30

μ2 = 1.2 - 1.2( β-30)/30

 

β > 60° --> μ1 = μ2 = 0
III
 Charge de neige répartie après redistribution et enlèvement partiel par le vent (vent fort à partir de 20 m/s)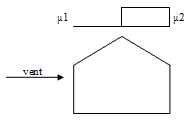

μ1 = 0

 

β ≤ 15° --> μ2 = 0

β > 15° --> cf cas II

 

 

 

4. de la prise en compte d'une éventuelle majoration s1 : cette majoration ne vise que les difficultés d'évacuation des eaux de pluie en présence de neige.

s1 = 20 daN/m² lorsque la pente nominale du fil de l'eau de la partie enneigée de toiture (noue par exemple) est inférieure ou égale à 3%.

s1 = 10 daN/m² lorsque cette pente est comprise entre 3 et 5%.

La zone de majoration s'étend dans toutes les directions sur une distance de 2m au-delà de la partie de toiture enneigée.

 

 

 

 

Au final la charge de neige s'écrit : s = μ s0 + s1