Ecriture de la matrice raideur d'une poutre encastrée/encastrée dans son repère local
La matrice raideur complète d'un élément poutre est obtenue par addition des 3 matrices explicitées dans la section précédente "Les approximations nodales" (traction, flexion et torsion).
Il s'agit donc d'une matrice 12x12 : 2 inconnues pour la matrice traction, 2 x 4 pour les matrices flexion (2 plans de flexion) et 2 pour la matrice torsion. Ces 12 inconnues correspondent simplement aux 6 variables pour chacun des 2 noeuds de l'élément poutre (3 déplacements + 3 rotations par noeud).
On rappelle que les conventions de notation d'inertie sont les suivantes : Iy est l'inertie forte, et Iz l'inertie faible (dans le repère local de la poutre).
Avec ces notations, la matrice complète s'écrit (la matrice étant symétrique, seule la partie triangulaire supérieure est explicitée) :
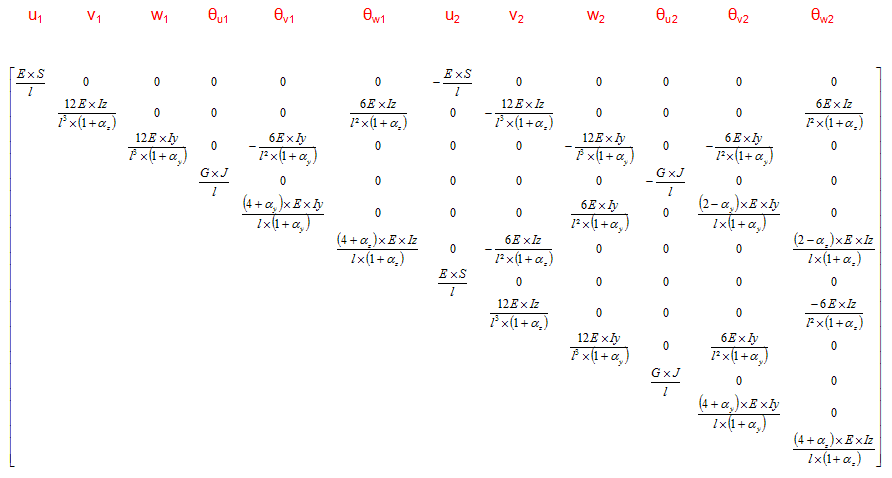
Matrice raideur d'un élément relâché (articulé/articulé, type contreventement, ou articulé/encastré)
![]() Pour obtenir la matrice raideur d'un élément treillis (élément articulé/articulé, ne travaillant qu'en traction/compression), il suffit d'annuler tous les termes autres que ceux de traction : on rappelle que les termes de traction sont (1,1), (1,7), (7,1) et (7,7) (le 1er chiffre étant celui de la ligne, et le 2ème celui de la colonne).
Pour obtenir la matrice raideur d'un élément treillis (élément articulé/articulé, ne travaillant qu'en traction/compression), il suffit d'annuler tous les termes autres que ceux de traction : on rappelle que les termes de traction sont (1,1), (1,7), (7,1) et (7,7) (le 1er chiffre étant celui de la ligne, et le 2ème celui de la colonne).
![]() Pour obtenir la matrice raideur d'un élément articulé/encastré, il suffit de remplacer les termes de flexion par ceux définis dans Approximations nodales>Flexion (cf en bas de la page).
Pour obtenir la matrice raideur d'un élément articulé/encastré, il suffit de remplacer les termes de flexion par ceux définis dans Approximations nodales>Flexion (cf en bas de la page).
Remarques sur la matrice raideur
![]() Cette matrice peut se déchiffrer de cette façon : un élément (i,j) correspond à la force en i due à un déplacement unitaire en j.
Cette matrice peut se déchiffrer de cette façon : un élément (i,j) correspond à la force en i due à un déplacement unitaire en j.
![]() Tous les éléments diagonaux sont positifs car le déplacement et la force qui le cause en un point sont toujours de même sens.
Tous les éléments diagonaux sont positifs car le déplacement et la force qui le cause en un point sont toujours de même sens.
![]() La matrice est singulière (non inversible) car en absence d'appuis elle décrit un système instable.
La matrice est singulière (non inversible) car en absence d'appuis elle décrit un système instable.
![]() Si on ne prend pas en compte les déformations dues au cisaillement, les termes en alpha dans la matrice sont nuls, et on retrouve alors l'expression classique de la matrice raideur.
Si on ne prend pas en compte les déformations dues au cisaillement, les termes en alpha dans la matrice sont nuls, et on retrouve alors l'expression classique de la matrice raideur.
![]() Dans un repère cartésien (u,v,w), l'effort suivant v induit une rotation positive suivant w, et l'effort suivant w induit une rotation négative suivant v. C'est pour cette raison que dans le plan flexionnel (v,
θw), les termes de la matrice correspondent au signe près à ceux décrits dans l'approximation nodale de la flexion. En revanche, dans le plan flexionnel (w,
θv), on change le signe des termes en
θv (sauf les éléments en
θv pour la ligne et pour la colonne, car moins fois moins font plus).
Dans un repère cartésien (u,v,w), l'effort suivant v induit une rotation positive suivant w, et l'effort suivant w induit une rotation négative suivant v. C'est pour cette raison que dans le plan flexionnel (v,
θw), les termes de la matrice correspondent au signe près à ceux décrits dans l'approximation nodale de la flexion. En revanche, dans le plan flexionnel (w,
θv), on change le signe des termes en
θv (sauf les éléments en
θv pour la ligne et pour la colonne, car moins fois moins font plus).
Ecriture de la matrice masse d'une poutre encastrée/encastrée dans son repère local
La matrice masse de Euler-Bernoulli (pas de prise en compte des déformations d'effort tranchant et de l'inertie rotationnelle) s'écrit :
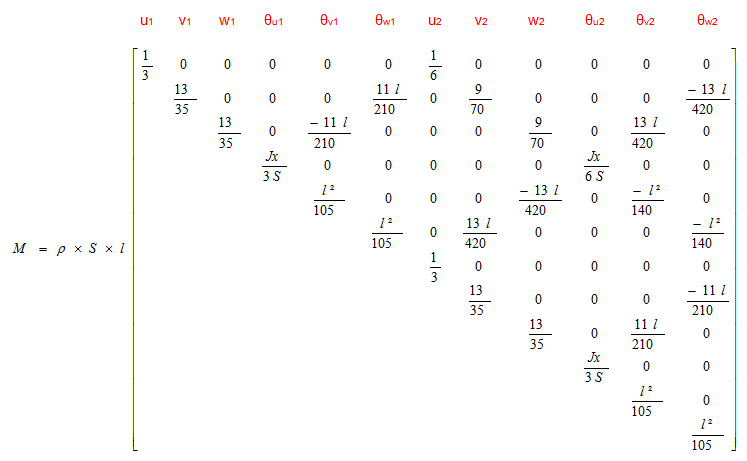
Avec les déformations d'effort tranchant et l'inertie rotationnelle, l'expression de la matrice est plus complexe.
Ci-dessous l'écriture 4x4 de la partie flexionnelle Iz (rz est le rayon de giration) :
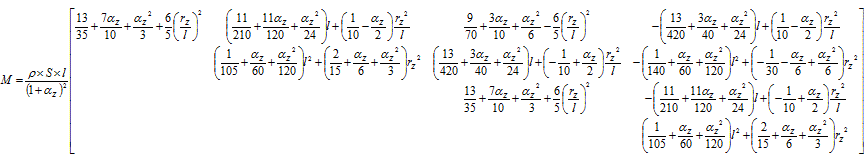
(source : "Theory of Matrix Structural Analysis" de J.S. Przemieniecki)
Rotation du repère (passage du repère local au repère global)
Les matrices précédentes s'écrivent dans le repère local de la poutre, puis, par rotation du repère, dans le repère global pour assemblage avec les matrices des autres éléments de la structure.
Les repères local et global sont décrits dans le schéma ci-dessous :
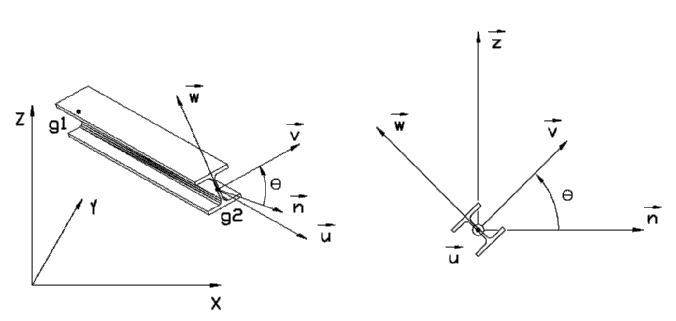
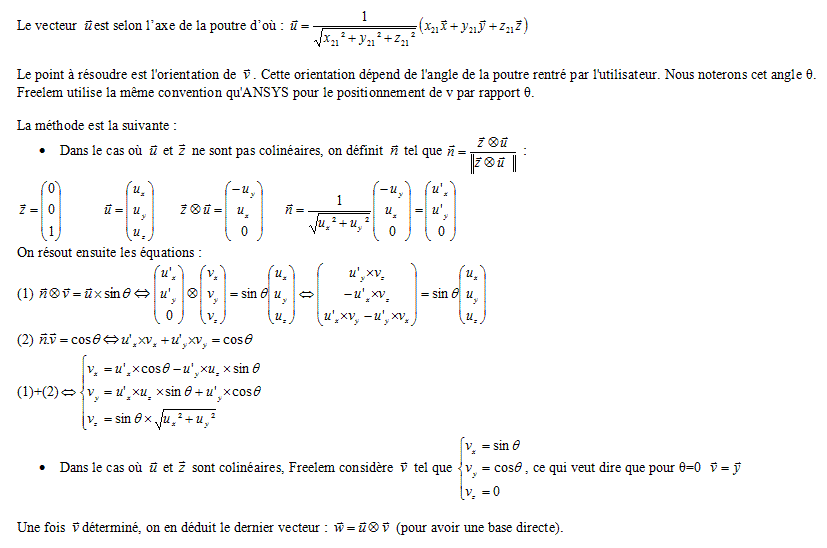
| La matrice de rotation de l'élément s'écrit finalement : | 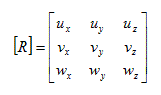 |
Une fois la matrice rotation constituée (on reconduit cette matrice 4 fois pour avoir la matrice finale 12x12 de changement de repère), il ne reste plus qu'à effectuer le changement de repère. En considérant [K'] la matrice raideur dans le repère local et [K] la matrice raideur dans le repère global, ce changement s'écrit :
![]()