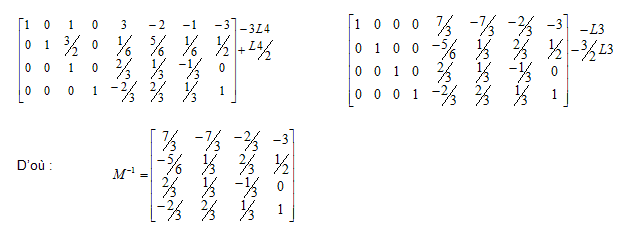Freelem - Théorie - Résolution statique

Nombre d'inconnues

La dimension de la matrice raideur (matrice carrée) correspond au nombre d'inconnues. A chaque noeud de la structure sont associées 6 inconnues : 3 déplacements et 3 rotations. Les éventuels blocages se soutraient au nombre d'inconnu. Ainsi, un noeud encastré correspond à 0 inconnue, un noeud articulé à 3 (3 rotations).

Exemple : soit une structure composée de 5 noeuds dont 1 est encastré et 1 rotulé.

Le nombre total d'inconnues est égal à : n = 5 x 6 - 6 - 3 = 21

Equation matricielle

La résolution par la méthode des éléments finis utilisée dans Freelem repose sur l'équation matricielle suivante :

F = K X

avec F = vecteur des efforts et moments externes appliqués à la structure

K = matrice raideur globale de la structure

X = vecteur des déplacements et rotations des noeuds de la structure

Le vecteur F et la matrice K sont calculés par le logiciel en fonction des données utilisateur. Le vecteur X est obtenu par inversion de l'équation : X = K(-1) F

La matrice raideur K est inversée par la méthode du pivot de Gauss, présentée ci-dessous.

Pivot de Gauss

Une fois la matrice raideur construite, son inversion est nécessaire pour déterminer les différentes inconnues constituées par les déplacements et de rotations.

Pour ceci, la méthode de pivot de Gauss, avec action uniquement sur les lignes, est utilisée. Cette méthode s’articule de la façon suivante :

Soit M une matrice.

1 ère étape : juxtaposition de M et de la matrice identité.

Puis par colonne (boucle i) :

2 ème étape : on cherche le pivot (1 er élément non nul, à partir de la ligne i) à position ligne = j

3 ème étape : échange des lignes i et j si i ≠j

4 ème étape : on divise la ligne i par la valeur du pivot afin que le pivot vale 1

5 ème étape : annulation de tous les termes en-dessous du pivot par soustraction des lignes

Fin de la boucle sur les colonnes à le résultat est une matrice triangulaire supérieure avec que des 1 sur la diagonale.

6 ème étape : réduction de la matrice M à pour annuler les termes au-dessus de la diagonale (toujours par soustraction de lignes)

7 ème étape : récupération de la matrice inverse (en lieu et place de la matrice identité juxtaposée en 1 ère étape).

Exemple pour illustrer le fonctionnement de l’algorithme :

2 ème étape sur la colonne 1 : le pivot est sur la 1 ère ligne

3 ème étape et 4 ème étape sur la colonne 1 : rien à faire

5 ème étape sur la colonne 1 : annulation des termes sous le pivot

On passe maintenant à la colonne 4 :

Le pivot est 1. Il n’y a donc rien à faire.

On a une matrice triangulaire supérieure (en ne considérant que les 4 premières colonnes, correspondant à la matrice initiale) avec une diagonale de 1.

Il reste donc à réduire cette matrice en annulant les termes au-dessus de la diagonale de 1. On commence par la dernière colonne (pour la colonne i considérée on se sert de la ligne i comme ligne pivot).